前言
这节课我们会学习一种方法,通过它我们可以证明非上下文无关语言。这个方法你会觉得非常熟悉,因为它和我们在第5节课证明非正则语言的方法是类似的。
知识点
上下文无关语言的泵引理
沿着我们在第五节课证明非正则语言的讨论时的思路,我们提出一个适用于上下文无关语言的泵引理变体。
这个引理的证明自然不同于正则语言的泵引理证明,但是基本思路是相似的。主要思路是如果你有通过某个上下文无关语法生成的特定字符串,知道推导出它的分析树,这个树的有足够的深度,那么一定存在某个变量在从根节点到叶节点的路径上多次出现,我们找到了一种类似于正则语言泵引理的泵效应。
引理10.1(上下文无关语言的泵引理). 已知$\Sigma$是一个字母表,$A\in\Sigma^{*}$是一个上下文无关语言。存在一个正整数$n$(称作泵长度)拥有以下属性。对于每个字符串$w\in A$并且$|w|\geq n$,选择一些字符串$u,v,x,y,z\in\Sigma^{*}$可以写出$w=uvxyz$使得
- $vy\neq \varepsilon$,
- $|vxy|\leq n$,
- 对于所有$i\in\mathbb{N}$有$uv^ixy^iz\in A$.
证明:已知$A$是上下文无关的,我们知道一定存在一个乔姆斯基范式的CFG $G$使得$A=L(G)$。让$m$表示$G$中变量的数量。我们将证明$n=2^m$时所有引理中声明的属性都有效。
假设字符串$w\in A$满足$|w|\geq n=2^n$。因为$G$是乔姆斯基范式,每个$w$的分析树有恰好$2|w|-1$个变量和$|w|$个叶子节点。在此之后我们选择这些分析树中的任意一个,把它叫做树$T$。为了方便证明,关于$T$的大小有很重要的一点是它至少有$2^m$个变量节点。这是对的,因为$2|w|-1\geq 2\cdot 2^m-1\geq 2^m$。事实上,最后一个不等是严格的,因为$m\geq 1$,但是这对证明没有任何影响。因为变量节点的数量至少是$2^m$,$T$中一定存在一条从根节点到叶节点的路径至少有$m+1$个变量节点 — 因为如果这些路径只有$m$或者更少的变量节点,那么整个树种最多只会有$2^m-1$个变量节点。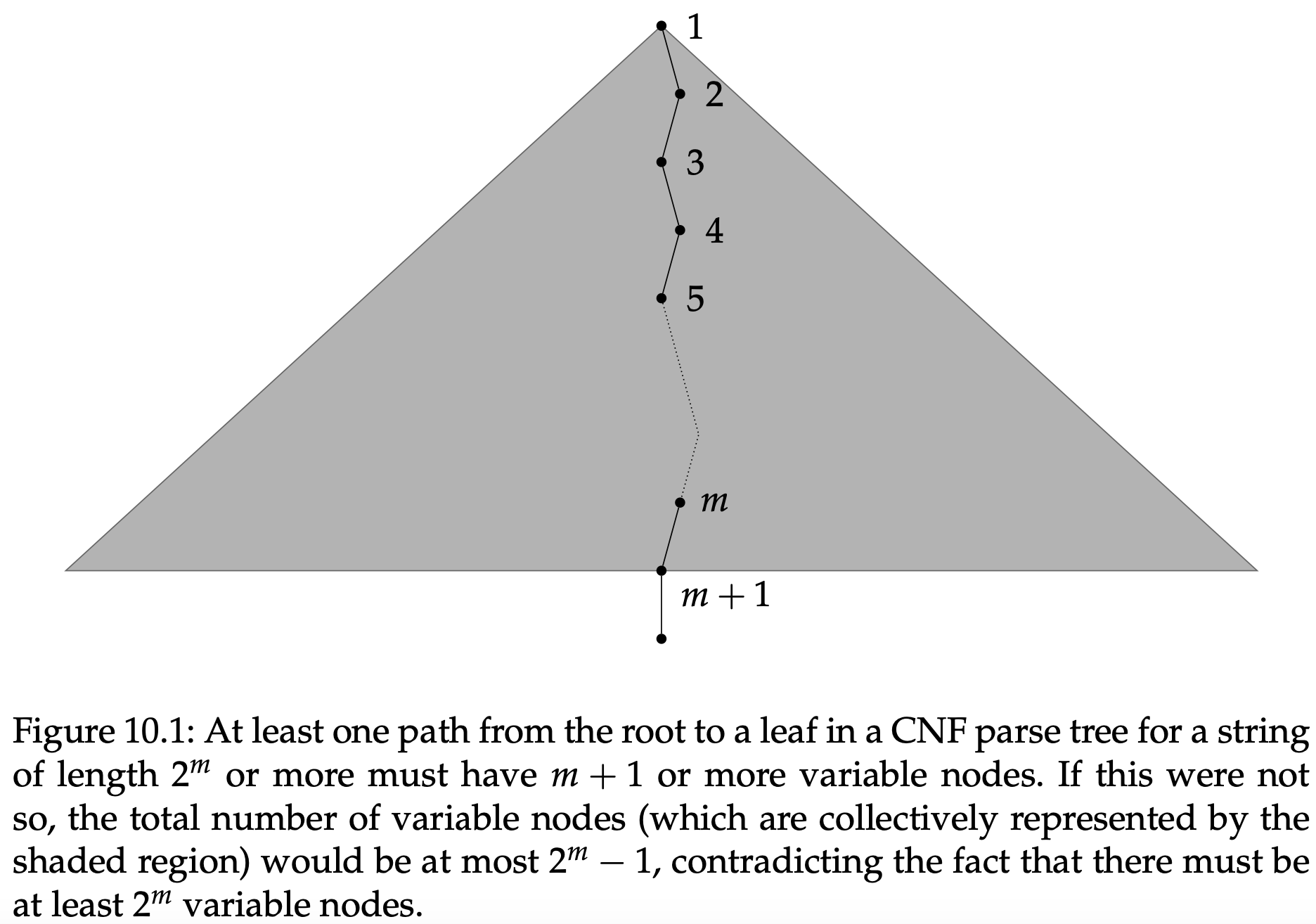
接下来选择任意$T$中从根节点到叶节点长度最大的路径。(也许有很多选择,但是任选一个就行)我们知道至少有$m+1$个变量会出现在这个路径中,正如上面所讨论的 — 而且因为总共只有$m$个不同的变量,那么至少有一个变量在这个路径中出现了多次。事实上,我们知道某个变量(称作$X$)一定会我们选择的路径中的最靠近叶节点的位置第二次出现。让$T_1$和$T_2$表示最底部出现的$X$作为根节点的子树,$T_2$是两个中较小的。顺便说说我们选择的这两个树,我们$T_2$是$T_1$的真子树,而且$T_1$不是很大:每个从$T_1$根节点出发到叶节点的路径中变量节点不超过$m+1$个,因此$T_1$的叶节点不超过$2^m=n$个。
现在,用$x$表示$T_2$(从$X$开始的分析树)生成的字符串,$x$和$y$表示$T_1$生成的字符串分别在$T_2$左边和右边的部分,$vxy$则表示$T_1$(也是从$X$开始的分析树)生成的字符串。最后,$u$和$z$表示$T$生成的字符串分别在$T_1$左边和右边的部分,那么$w=uvxyz$。图10.2阐述了字符串$u,v,x,y,z$和$T,T_1,T_2$的关系。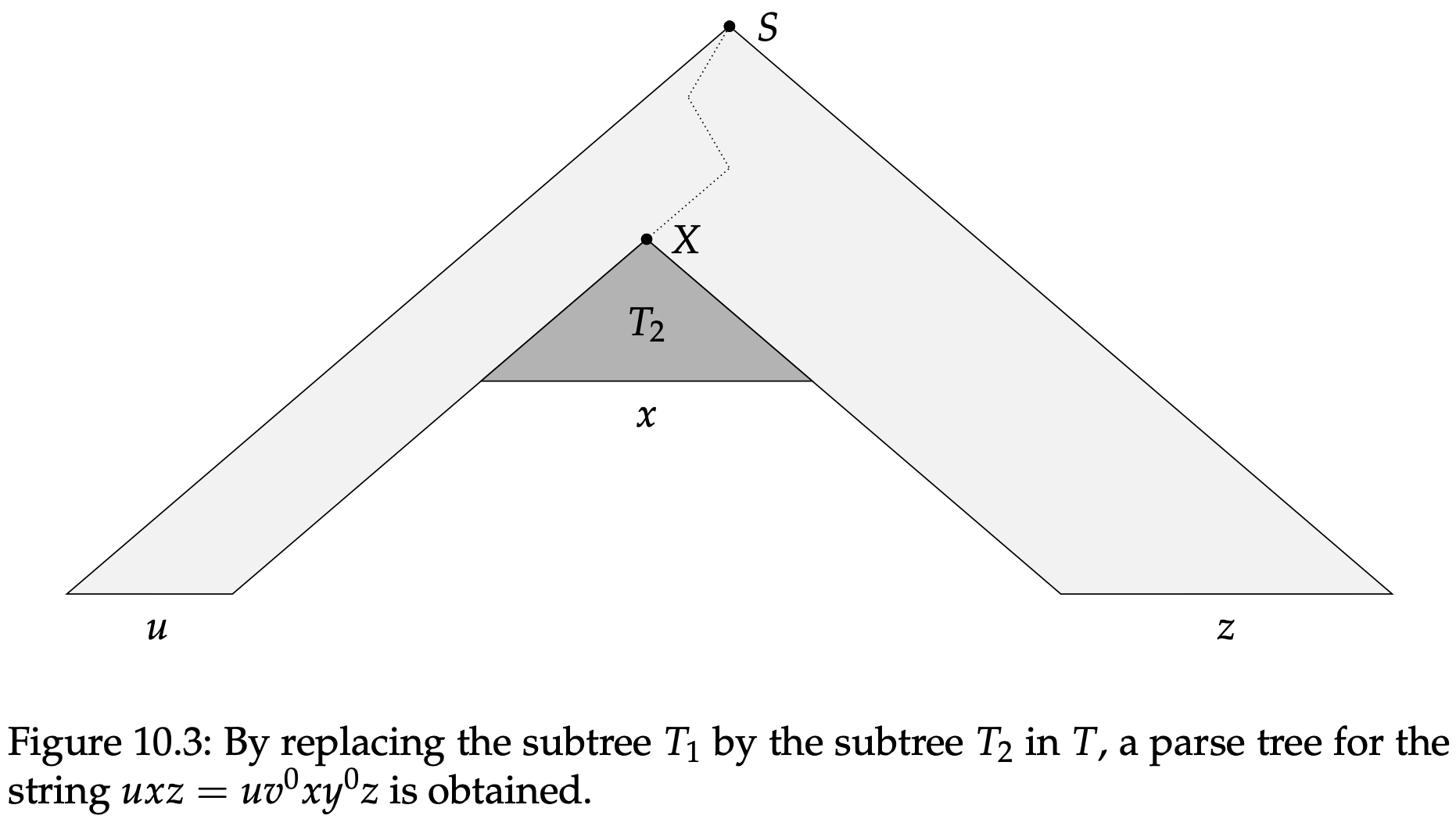
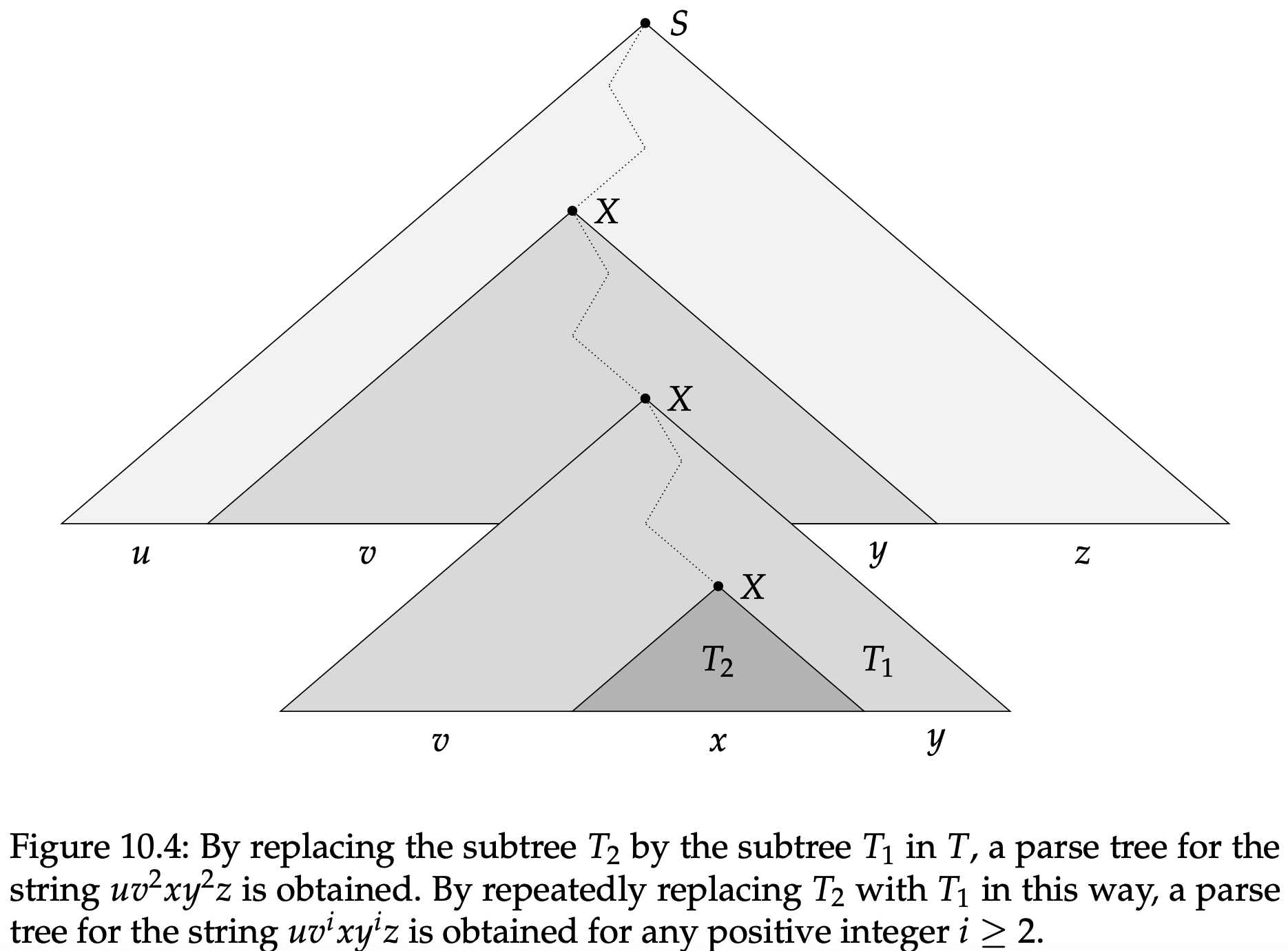
剩下的就是要证明$u,v,x,y,z$具有引理声明中要求的属性。让我们先来证明对于所有$i\in\mathbb{N}$有$uv^ixy^iz\in A$。为了弄清$uxz=uv^0xy^0z\in A$,我们观察到通过将$T_1$替换成$T_2$,能得到一个有效的分析树,如图10.3所示。这个替换是可行的,因为$T_1$和$T_2$的根节点都是变量$X$。同样的思路,我们可以得出$uv^2xy^2z\in A$,因为我们可以通过复制一个$T_2$来替换$T_1$得到一个有效的的分析树,如图10.4所示。通过重复复制$T_1$来替换$T_2$,我们就能获得$uv^ixy^iz$的分析树。
接下来,$vy\neq \varepsilon$这个事实源自于一个字符串的每个分析树所对应的乔姆斯基范式CFG的大小都是相同的。因此图10.3和图10.2生成的字符串不可能相同,因为两个树的变量节点的数量不同。这说明$uvxyz\neq uxz$,也就是说$vy\neq \varepsilon$。
最后,因为$T_1$的叶节点数量最多是$2^m=n$,那么$|vxy|\leq n$,综上证明就完成了。
使用上下文无关语言的泵引理
现在我们手中有了上下文无关语言的泵引理,我们可以证明某个语言是非上下文无关的。这个方法和我们第5节课中证明某个语言是非正则的类似。比如下面这个命题。
命题10.2. 已知$\Sigma=\{0,1,2\}$,语言$A$的定义如下:
语言$A$是非上下文无关的。
证明:我们使用反证法,假设$A$是上下文无关的。由上下文无关语言的泵引理可知,$A$一定存在一个泵长度$n$。接下来的证明中我们会假设一个泵长度$n$。让
其中$w\in A$并且$|w|=3n\geq n$,然后泵引理确保了一定存在字符串$u,v,x,y,z\in\Sigma^{*}$使得$w=uvxyz$,而且引理中的三个属性都生效:(i)$vy\neq\varepsilon$,(ii)$|vxy|\leq n$,并且(iii)对于所有$i\in\mathbb{N}$有$uv^ixy^iz\in A$。
现在,已知$|vxy|\leq n$,那么符号0和1不可能同时出现在$vy$中;0和1之间的距离太远了。另外,$\Sigma$中至少有一个符号出现在$vy$中,因为这个字符串是非空的。这表示字符串
中要么是1或者2的数量少于0,要么是0或者1的数量少于2。也就是,如果符号0没出现在$vy$中,那么一定有
而如果符号2没出现在$vy$中,那么一定有
然而这时有矛盾的,因为根据引理的第三个属性$uv^0xy^0z=uxz$是属于$A$的。
由于这个矛盾,我们得出$A$是费上下文无关的,证毕。
在某些情况下,就像下面这个命题,一个语言能被证明非上下文无关的方式和它被证明非正则的方式一模一样。
命题10.3. 已知$\Sigma=\{0\}$,回想一下这个语言
它在第5节课中定义过。这个语言是非上下文无关的。
证明:我们使用反证法,假设$SQUARE$是上下文无关的。根据上下文无关语言的泵引理,$SQUARE$一定存在一个泵长度$n\geq 1$使得引理中的三个属性有效。接下来的证明中我们会假设一个泵长度$n$。定义
我们知道$w\in SQUARE$和$|w|=n^2\geq n$,那么泵引理告诉我们一定存在$u,v,x,y,z\in\Sigma^{*}$使得$w=uvxyz$,而且一下三个条件生效:
- $vy\neq \varepsilon$,
- $|vxy|\leq n$,
- 对于所有$i\in\mathbb{N}$有$uv^ixy^iz\in SQUARE$.
字母表$\Sigma^{*}$中只有一个符号,所以$vy=0^k$,其中$k\in\mathbb{N}$。因为$vy\neq \varepsilon$而且$|vy|\leq |vxy|\leq n$,那么就有$1\leq k\leq n$。观察这个
其中$i\in\mathbb{N}$。特别地,如果我们选择$i=2$,那么我们有
然而因为$1\leq k\leq n$,$n^2+k$不是一个完全平方。这是因为$n^2+k$大于$n^2$,但是$n^2$的下一个完全平方数是
这个数明显大于$n^2+k$,因为$k\leq n$。字符串不包含于$SQUARE$,这与泵引理的第三个条件矛盾,它要求对于所有$i\in\mathbb{N}$有$uv^ixy^iz\in SQUARE$。
得到这个矛盾后,我们得出$SQUARE$是非上下文无关的,证毕。
注意10.4 我们不会具体证明,但是这个结果看起来每个基于单字符字母表的上下文无关语言一定是正则的。通过这个事实与$SQUARE$是一个非正则语言联系起来,我们得到了$SQUARE$是费上下文无关的另一种证明。
这里还有一个使用泵引理证明非上下文无关语言的例子。这个例子中会有点混乱,因为它有很多种情况需要考虑。当然,这就需要我们在所有情况下都得到一个矛盾才能完成一个有效的反证,所以要牢记这一点。
命题10.5. 已知$\Sigma\{0,1,\sharp\}$,定义一个基于$\Sigma$的语言$B$如下:
语言$B$是非上下文无关的。
证明:我们使用反证法,假设$B$是上下文无关的。根据上下文无关语言的泵引理,$B$一定存在一个泵长度$n$。在余下的证明中我们会假定这么一个泵长度$n$。让
我们知道$w\in B$(因为$0^n1^n$是它自身的一个子串),还有$|w|=4n+1\geq n$。因此泵引理保证了一定存在字符串$u,v,x,y,z\in\Sigma^{*}$使得$w=uvxyz$,而且引理中的三个属性有效:(i)$vy\neq\varepsilon$,(ii)$|vxy|\leq n$,和(iii)对于所有$i\in\mathbb{N}$有$uv^ixy^iz\in B$。
符号$\sharp$只会在$w$中出现一次,所以他一定是出现在字符串$u,v,x,y,z$中的一个。我们分别考虑每种情况:
- $\sharp$出现在$u$中。这种情况下$v$和$y$的所有字符都出现在$\sharp$的右边。那么对于整数$j,k$一定有$j+k\geq 1$,因为从$w$中移除$v$和$y$我们至少要从$\sharp$的右边移除一个符号(但是左边的符号数量不变)。字符串(10.13)没有包含在$B$中,这与我们第三个属性冲突,所以在这种情况下我们得到了一个矛盾。
- $\sharp$出现在$v$中。这种情况很简单:因为$\sharp$在$v$中,字符串$uv^0xy^0z=uxz$不包含符号$\sharp$,所以他不可能在$B$中。这与第三个属性冲突,所以在这种情况下我们得到了一个矛盾。
- $\sharp$出现在$x$中。这种情况下,我们知道$vxy=1^j\sharp 0^k$,其中整数$j,k$一定有$j+k\geq 1$。而$vxy$采用这种形式的原因是因为$|vxy|\leq n$,所以这个子串不可能在包含$\sharp$的情况下,即接触到第一个0的区块,有接触到最后一个1的区块,而为什么$j+k\geq 1$的原因则是$vy\neq \varepsilon$。如果$n\geq 1$,我们选择$i=2$来获得矛盾。因为它不包含在$B$中,因为$\sharp$左边的1比右边的多。如果$k\geq 1$,那么我们选择$i=0$来获得矛盾:我们有他不包含于$B$中,因为$\sharp$左边的0比右边的多。
- $\sharp$出现在$x$中。这个情况获得矛盾的条件和情况2相同。
- $\sharp$出现在$z$中。这种情况下$v$和$y$的符号都出现在$\sharp$的左边。因为$vy\neq \varepsilon$,那么其中字符串$r$的长度明显超过了$2n$。字符串不包含在$B$中,这与第三个属性冲突,所以在这种情况下我们得到了一个矛盾。
所有情况下我们都得到了矛盾,我们得出这个假设整体上是矛盾的 — $B$是非上下文无关的,证毕。
非上下文无关语言和闭包属性
在上节课中我们说上下文无关语言在交集和补集运算下不是闭合的。也就是存在上下文无关语言$A$和$B$使得$A\cap B$和$\overline{A}$都不是上下文无关的。我们现在可以验证这些声明了。
首先,让我们考虑交集的情况。假设我们定义语言$A$和$B$如下:
这的确是两个上下文无关语言 — 生成$A$的一个CFG是
而生成$B$的一个CFG是
另外,交集$A\cap B$是非上下文无关的,这个我们在命题10.2已经证明过了。
现在我们已经证明了上下文无关语言在交集运算下不是闭合的,紧接着我们就知道上下文无关语言在补集运算下也不是闭合的。这是因为我们已经知道上下文无关语言在并集运算下是闭合的,如果它们在补集运算下也是闭合的,由德摩根定律可知交集运算也应该是闭合的。
最后,让我来看看有时候我们可以使用闭包属性来证明某个语言是非上下文无关的。比如,考虑这个语言
当然使用泵引理可以证明$D$是非上下文无关的,用法类似于命题10.2。不过还有一个更简单的方法来得出这个事实。我们假设$D$是上下文无关的。因为一个上下文无关语言和一个正则语言的交集一定是上下文无关的,也就是说$D\cap L(0^{*}1^{*}2^{*})$是上下文无关的(因为因为$L(0^{*}1^{*}2^{*})$是一个正则表达式所匹配的语言)。然而
我们已经知道它是非上下文无关的了。有了这个矛盾,我们得出$D$是非上下文无关的,证毕。